Year 13’s James Tan sealed his long and glittering record of success in Mathematics competitions at QE with a perfect score in this year’s Senior Maths Challenge (SMC).
He was one of nine Sixth Form mathematicians who performed so strongly in the challenge that they qualified for the élite British Mathematical Olympiad.
James’s tally of 125 out of 125 secured him the Best in School title, while Abhinav Santhiramohan, with a score of 112 out of 125 was Best in Year 12. To qualify for the Olympiad, candidates had to score at least 108 points.
Assistant Head of Mathematics Wendy Fung said: “James has scored perfect, or near-perfect, marks in every Maths Challenge he has sat, from Year 7 to Year 13. He has done phenomenally well throughout his School career and is so unassuming about his successes.”
In addition to the Olympiad successes, a further 29 boys qualified for the challenge’s other follow-on round, the Senior Kangaroo, which required a score of at least 91 points.
A total of 136 QE sixth-formers sat the challenge, which involved answering 25 multiple-choice questions in 90 minutes.
The top 40% of SMC entrants nationally in the country receive certificates with gold, silver and bronze awarded in the ratio of 1:2:3. At QE, however, there were 38 gold certificates, 65 silver and 22 bronze, which means that 92% of the School’s participants gained certificates.
“We are very pleased with the boys’ success at the SMC,” Miss Fung. “The challenge provides an opportunity for our senior boys to hone their problem-solving skills with fun, yet challenging, questions, and we are grateful to the UK Maths Trust for providing these opportunities. Many congratulations to Years 12 & 13 – we look forward to receiving the Olympiad and Kangaroo results in due course.”
She added that Abhinav had said that he particularly enjoyed solving the following question in the challenge (answer below):
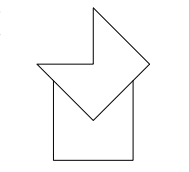Question: Two congruent pentagons are each formed by removing a right-angled isosceles triangle from a square of side-length 1.
The two pentagons are then fitted together as shown. What is the length of the perimeter of the octagon formed?
A: 4
B : 4 + 2 √ 2
C: 5
D: 6 − 2 √ 2
E: 6
- Answer: E: 6
Explanation: The perimeter of the octagon is made from four long sides, two medium-length sides and two short sides. The long sides are given to be of length 1. The medium-length sides have length 1 √ 2 , using Pythagoras’ Theorem on the right-angled triangle which was removed from the original square. Therefore the length of each short side is 1 − 1 √ 2 . In total the perimeter has length 4 × 1 + 2 × 1 √ 2 + 2 × (1 − 1 √ 2 ) = 6.